🧪 2307 도로검문
난이도 : 🌟 골드 1
유형 : 다익스트라
https://www.acmicpc.net/problem/2307
📝 문제

그림 1은 어떤 도시의 주요 지점과 그 지점들 간의 이동시간을 나타낸 그래프이다. 그래프의 노드는 주요 지점을 나타내고 두 지점을 연결한 도로(에지)에 표시된 수는 그 도로로 이동할 때 걸리는 분 단위의 시간을 나타낸다. 두 지점 a와 b를 연결하는 도로는 도로(a,b)로 표시한다.
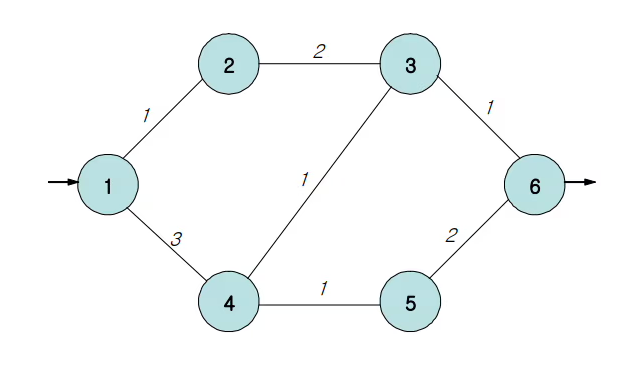
그림 1
예를 들어 도로(1,2)와 도로(2,3)를 통하여 지점1에서 지점3으로 갈 때 걸리는 시간은 3분이다. 도로는 모두 양방향이라고 가정하므로 도로(a,b)와 도로(b,a)를 지날 때 걸리는 시간은 항상 같다고 한다.
어떤 범죄용의자가 입력 데이터에 표시된 도시로 진입하여 이 도시를 가장 빠른 시간 내에 빠져나가고자 한다. 그런데 이 사실을 알고 있는 경찰이 어떤 하나의 도로(에지)를 선택하여 이 도로에서 검문을 하려고 한다. 따라서 용의자는 이 도로를 피해서 가장 빠르게 도시를 탈출하고자 한다. 이 경우 경찰이 검문을 위하여 선택하는 도로에 따라서 용의자의 가장 빠른 탈출시간은 검문이 없을 때에 비하여 더 늘어날 수 있다.
문제는 도로검문을 통하여 얻을 수 있는 탈출의 최대 지연시간을 계산하는 것이다. 추가설명은 다음과 같다.
- 두 개의 지점을 직접 연결하는 도로가 있는 경우, 그 도로는 유일하다.
- 도시의 지점(노드)은 1에서 N번까지 N개의 연속된 정수로 표시된다.
- 용의자가 도시에 진입하는 지점은 항상 1번이고 도시를 빠져 나가기 위하여 최종적으로 도달해야하는 지점은 항상 N번 지점이다.
- 용의자는 검문을 피해서 가장 빨리 도시를 빠져나가고자 하고, 경찰은 적절한 도로를 선택하여 이 용이자들의 탈출시간을 최대한 지연시키고자 한다.
- 각 도시 지점 간을 이동하는 시간은 항상 양의 정수이다.
입력 도시의 도로망에 따라서 경찰이 어떤 도로를 막으면 용의자는 도시를 탈출하지 못할 수도 있다. 이 경우 검문으로 인하여 지연시킬 수 있는 탈출시간은 무한대이다. 이 경우에는 -1을 출력해야 한다.
그림 1에서 볼 때 검문이 없을 경우 용의자가 도시를 탈출하는데 걸리는 시간은 4분이다. 만일 경찰이 도로(4,3)을 막으면 그 탈출시간을 지연시킬 수 없으므로 지연시간은 0이다. 만일 도로(2,3)을 막으면, 용의자들이 가장 빠르게 탈출할 수 있는 시간은 5분이므로 탈출지연시간은 1분이고, 도로(3,6)을 막으면 탈출지연시간은 2분이다.
여러분은 입력 데이터에 표시된 도로망을 읽고, 경찰이 한 도로를 막고 검문함으로써 지연시킬 수 있는 최대시간을 정수로 출력하여야한다. 만일 지연효과가 없으면 0을 출력해야하고, 도시를 빠져나가지 못하게 만들 수 있으면(지연시간이 무한대) -1을 출력해야 한다.
입력
첫 줄에는 지점의 수를 나타내는 정수 N(6 ≤ N ≤ 1000)과 도로의 수 M(6 ≤ M ≤ 5000)이 주어진다. 그 다음 이어 나오는 M개의 각 줄에는 도로(a, b)와 그 통과시간 t가 a b t 로 표시된다. 단 이 경우 a < b 이고 1 ≤ t ≤ 10000이다.
출력
경찰이 하나의 도로를 막음으로써 지연시킬 수 있는 최대 시간을 정수로 출력한다. (단, 그 지연시간이 무한대이면 -1을 출력해야 한다.)
🧐 핵심 로직
1) 최소한으로 시간을 소비하고 목적지에 도달해야 하기 때문에 PriorityQueue를 활용한다.
1 - a) 새로운 경로를 발견했을 때 ) pq에 추가할 때 현재까지의 소요 시간 + 새 경로의 소요 시간을 해준다.
1 - b) 기존 경로보다 빠른 경로를 발견했을 때 ) pq에 추가할 때 새로 계산된 더 짧은 소요 시간으로 갱신한다.
2) 그래프를 탐색할 때마다 각 노드까지의 최소 소요 시간을 time 배열에 입력해둔다.
3) 2번부터 n-1번 도시를 막았다고 가정하고 다익스트라 알고리즘을 실행한다. 이 중 가장 오래 걸리는 시간을 res에 저장한다.
4) 막는곳 없이 1번에서 n번으로 가는 최단 경로를 계산하여 ans에 저장한다.
5) res와 ans의 차이를 출력한다. 만약 경로가 존재하지 않으면 -1을 출력한다.
💻 최종 코드 (796 ms)
import java.util.*;
import java.io.*;
public class Main {
static class Node implements Comparable<Node> {
int to, time;
Node(int to, int time) {
this.to = to;
this.time = time;
}
@Override
public int compareTo(Node o) {
return this.time - o.time;
}
}
static int n, m, res, ans;
static int INF = 987654321;
static int[] time;
static boolean[] visited;
static List<List<Node>> graph;
public static void main(String[] args) throws Exception {
// BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedReader br = new BufferedReader(new FileReader("input.txt"));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
res = Integer.MIN_VALUE;
graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int t = Integer.parseInt(st.nextToken());
graph.get(from).add(new Node(to, t));
graph.get(to).add(new Node(from, t));
}
for (int i = 2; i < n; i++) {
visited = new boolean[n + 1];
visited[i] = true;
dijkstra(1);
res = Math.max(res, time[n]);
}
visited = new boolean[n + 1];
dijkstra(1);
ans = time[n];
if (res == INF) {
System.out.println(-1);
} else {
System.out.println(res - ans);
}
br.close();
}
private static void dijkstra(int start) {
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start, 0));
visited[start] = true;
time = new int[n + 1];
Arrays.fill(time, INF);
time[start] = 0;
while (!pq.isEmpty()) {
Node now = pq.poll();
visited[now.to] = true;
for (Node next : graph.get(now.to)) {
if (!visited[next.to] && time[next.to] > time[now.to] + next.time) {
time[next.to] = time[now.to] + next.time;
pq.add(new Node(next.to, time[next.to]));
}
}
}
}
}'Hub Algorithm > 다익스트라' 카테고리의 다른 글
| [BOJ] 백준 1261 : 알고스팟 (java) (0) | 2024.06.12 |
|---|---|
| [BOJ] 백준 12834 : 주간 미팅 (java) (0) | 2024.06.01 |
| [BOJ] 백준 13424 : 비밀 모임 (java) (0) | 2024.04.15 |
| [BOJ] 백준 1753 : 최단경로 (java) (2) | 2024.03.16 |



