[CS 스터디 주소]
GitHub - noxknow/Tech_Interview_for_Beginner: 신입 개발자 CS 면접 대비 & SSAFY 11기 서울 CS 스터디 📖🔥
신입 개발자 CS 면접 대비 & SSAFY 11기 서울 CS 스터디 📖🔥. Contribute to noxknow/Tech_Interview_for_Beginner development by creating an account on GitHub.
github.com
🧪 Bubble Sort
🔹 Bubble Sort는 Selection Sort와 유사한 알고리즘으로 서로 인접한 두 원소의 대소를 비교하고, 조건에 맞지 않다면 자리를 교환하며 정렬하는 알고리즘 이다. 이름의 유래로는 정렬 과정에서 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어졌다고 한다.
버블 정렬은 첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬한다. 1회전을 수행하고 나면 가장 큰 자료가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 자료는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 자료까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.
⛓ Bubble Sort 예제
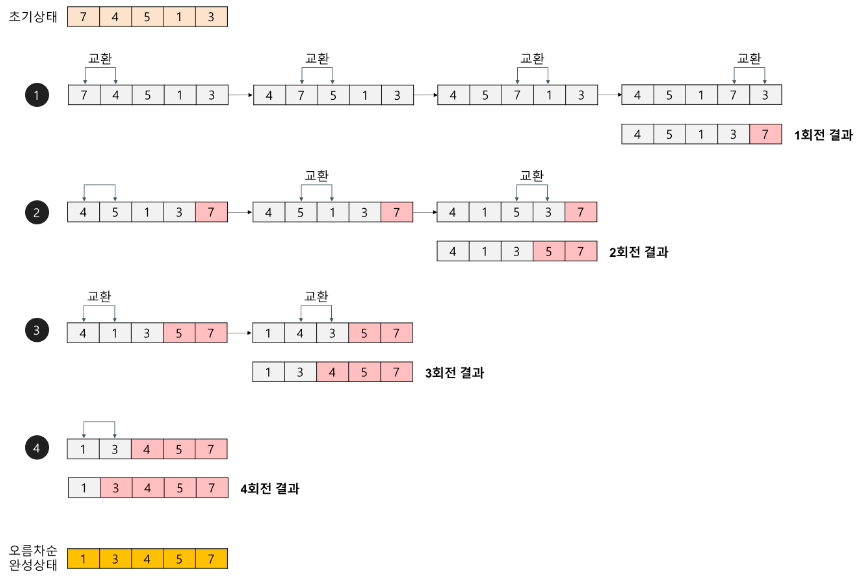

◈ 1회전
☉ 첫 번째 자료 7을 두 번째 자료 4와 비교하여 교환하고, 두 번째의 7과 세 번째의 5를 비교하여 교환하고, 세 번째의 7과 네 번째의 1을 비교하여 교환하고, 네 번째의 7과 다섯 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 네 번 비교한다. 그리고 가장 큰 자료가 맨 끝으로 이동하므로 다음 회전에서는 맨 끝에 있는 자료는 비교할 필요가 없다.
◈ 2회전
☉ 첫 번째의 4을 두 번째 5와 비교하여 교환하지 않고, 두 번째의 5와 세 번째의 1을 비교하여 교환하고, 세 번째의 5와 네 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 세 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 두 번째에 놓인다.
◈ 3회전
☉ 첫 번째의 4를 두 번째 1과 비교하여 교환하고, 두 번째의 4와 세 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 두 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 세 번째에 놓인다.
◈ 4회전
☉ 첫 번째의 1과 두 번째의 3을 비교하여 교환하지 않는다.
📚 Bubble Sort 특징
void bubbleSort(int[] arr) {
int temp = 0;
for (int i = n-1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
◈ 장점
☉ 구현이 매우 간단하다.
☉ 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않다. => 제자리 정렬(in-place sorting)
◈ 단점
☉ 시간복잡도가 최악, 최선, 평균 모두 O(n^2)으로, 굉장히 비효율적이다.
☉ 하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 이동하기 위해서는 배열에서 모든 다른 요소들과 교환되어야 한다. 특히 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환되는 일이 일어난다.
◈ 일반적으로 자료의 교환 작업(SWAP)이 자료의 이동 작업(MOVE)보다 더 복잡하기 때문에 버블 정렬은 단순성에도 불구하고 거의 쓰이지 않는다.
🍁 Bubble Sort 시간 복잡도
◈ 최악의 시나리오: O(N²)
☉ 비교: (N-1) + (N-2) + ... + 1 = N(N-1)/2번 (정렬이 되어있든, 안되어있든 똑같은 복잡도)
☉ 교환(swap): (N-1) + (N-2) + ... + 1 = N(N-1)/2번 (5인 배열의 경우 역순을 가정하면 4 + 3 + 2 + 1 = 10번의 교환을 수행)
◈ 최선의 시나리오: Ω(N²)
☉ 비교: (N-1) + (N-2) + ... + 1 = N(N-1)/2번
☉ 교환(swap): 0번
Bubble Sort는 정렬이 돼있던 안돼있던, 2개의 원소를 비교하기 때문에 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일하다.
🧪 Selection Sort
🔹 선택 정렬은 정렬되지 않은 데이터들에 대해 가장 작은 데이터를 찾아 가장 앞의 데이터와 교환해나가는 방식이다.
◈ 과정
☉ 주어진 리스트 중 최소값을 찾는다.
☉ 그 값을 맨 앞에 위치한 값과 교체한다. (패스(pass))
☉ 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
⛓ Selection Sort 예제
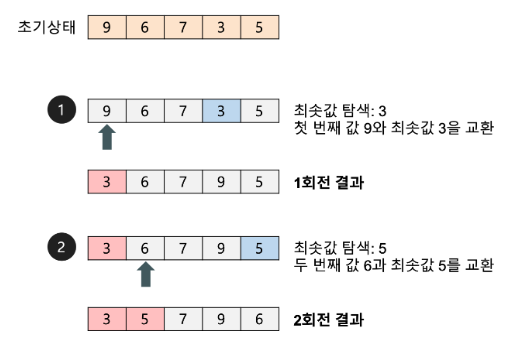
◈ 1회전
☉ 첫 번째 자료 9를 두 번째 자료부터 마지막 자료까지와 비교하여 가장 작은 값을 첫 번째 위치에 옮겨 놓는다. 이 과정에서 자료를 4번 비교한다.
◈ 2회전:
☉ 두 번째 자료 6을 세 번째 자료부터 마지막 자료까지와 비교하여 가장 작은 값을 두 번째 위치에 옮겨 놓는다. 이 과정에서 자료를 3번 비교한다.
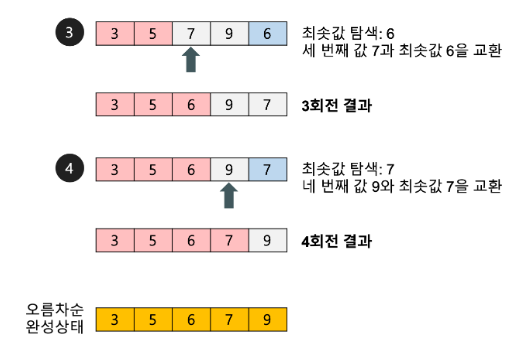
◈ 3회전:
☉ 세 번째 자료 7을 네 번째 자료부터 마지막 자료까지와 비교하여 가장 작은 값을 세 번째 위치에 옮겨 놓는다. 이 과정에서 자료를 2번 비교한다.
◈ 4회전:
☉ 네 번째 자료 9와 마지막에 있는 7을 비교하여 서로 교환한다.
📚 Selection Sort 특징
void selectionSort(int[] arr) {
int indexMin, temp;
for (int i = 0; i < arr.length-1; i++) { // 1.
indexMin = i;
for (int j = i + 1; j < arr.length; j++) { // 2.
if (arr[j] < arr[indexMin]) { // 3.
indexMin = j;
}
}
temp = arr[indexMin];
arr[indexMin] = arr[i];
arr[i] = temp;
}
System.out.println(Arrays.toString(arr));
}
◈ 장점
☉ Bubble sort와 마찬가지로 알고리즘이 단순하다.
☉ Bubble Sort와 마찬가지로 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
☉ 정렬을 위한 비교 횟수는 많지만, Bubble Sort에 비해 실제로 교환하는 횟수는 적기 때문에 많은 교환이 일어나야 하는 자료상태에서 비교적 효율적이다.
◈ 단점
☉ 시간복잡도가 최악, 최선, 평균 모두 O(n^2)으로, 비효율적이다.
☉ 불안정 정렬이다.
🍁 Selection Sort 시간 복잡도
◈ 비교 횟수
☉ 외부 루프: (n-1)번
☉ 내부 루프(최솟값 찾기): n-1, n-2, … , 2, 1 번
◈ 교환 횟수
☉ 외부 루프의 실행 횟수와 동일. 즉, 상수 시간 작업
◈ T(n) = (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)
🧪 Insertion Sort
🔹 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교 하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘
◈ 과정
☉ 정렬은 2번째 위치(index)의 값을 temp에 저장한다.
☉ temp와 이전에 있는 원소들과 비교하며 삽입해나간다.
☉ '1'번으로 돌아가 다음 위치(index)의 값을 temp에 저장하고, 반복한다.
⛓ Insertion Sort 예제
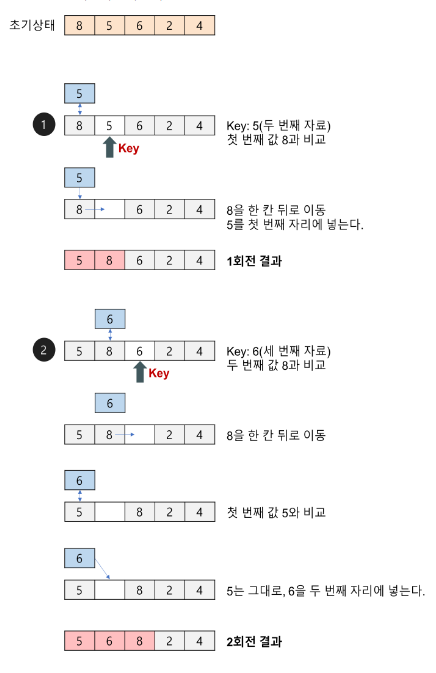
◈ 1회전 : 두 번째 자료인 5를 Key로 해서 그 이전의 자료들과 비교한다.
☉ Key 값 5와 첫 번째 자료인 8을 비교한다. 8이 5보다 크므로 8을 5자리에 넣고 Key 값 5를 8의 자리인 첫 번째에 기억시킨다.
◈ 2회전: 세 번째 자료인 6을 Key 값으로 해서 그 이전의 자료들과 비교한다.
☉ Key 값 6과 두 번째 자료인 8을 비교한다. 8이 Key 값보다 크므로 8을 6이 있던 세 번째 자리에 기억시킨다.
☉ Key 값 6과 첫 번째 자료인 5를 비교한다. 5가 Key 값보다 작으므로 Key 값 6을 두 번째 자리에 기억시킨다.
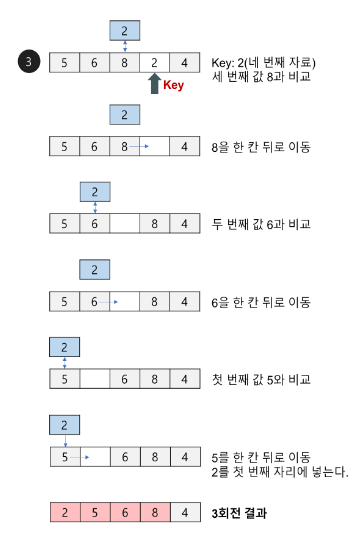
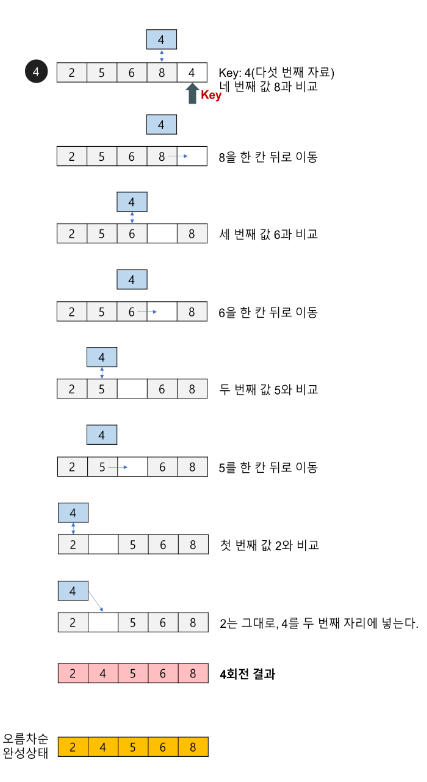
◈ 3회전: 네 번째 자료인 2를 Key 값으로 해서 그 이전의 자료들과 비교한다.
☉ Key 값 2와 세 번째 자료인 8을 비교한다. 8이 Key 값보다 크므로 8을 2가 있던 네 번째 자리에 기억시킨다.
☉ Key 값 2와 두 번째 자료인 6을 비교한다. 6이 Key 값보다 크므로 6을 세 번째 자리에 기억시킨다.
☉ Key 값 2와 첫 번째 자료인 5를 비교한다. 5가 Key 값보다 크므로 5를 두 번째 자리에 넣고 그 자리에 Key 값 2를 기억시킨다.
📚 Insertion Sort 특징
void insertionSort(int[] arr) {
for(int index = 1 ; index < arr.length ; index++){ // 1.
int temp = arr[index];
int prev = index - 1;
while( (prev >= 0) && (arr[prev] > temp) ) { // 2.
arr[prev+1] = arr[prev];
prev--;
}
arr[prev + 1] = temp; // 3.
}
System.out.println(Arrays.toString(arr));
}
◈ 장점
☉ 알고리즘이 단순하다.
☉ 대부분의 원소가 이미 정렬되어 있는 경우, 매우 효율적일 수 있다.
☉ 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
☉ Selection Sort나 Bubble Sort과 같은 O(n^2) 알고리즘에 비교하여 상대적으로 빠르다.
◈ 단점
☉ 평균과 최악의 시간복잡도가 O(n^2)으로 비효율적이다. (다만 최선의 경우 O(n))
☉ Bubble Sort와 Selection Sort와 마찬가지로, 배열의 길이가 길어질수록 비효율적이다.
🍁 Insertion Sort 시간 복잡도
◈ 최선의 경우
☉ 비교 횟수
☉ 이동 없이 1번의 비교만 이루어진다.
☉ 외부 루프: (n-1)번
☉ Best T(n) = O(n) (while문 안에 들어가지 않는 경우 key가 4번 인덱스라 가정하면 3번과의 비교만 수행하고 prev--;의 연산을 수행하지 못하므로 각 단계에서 1번의 비교만 이루어진다. 즉, n-1번의 비교와 교환이 없으므로 O(n))
◈ 최악의 경우(입력 자료가 역순일 경우)
☉ 비교 횟수
☉ 외부 루프 안의 각 반복마다 i번의 비교 수행
☉ 외부 루프: (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)
☉ 교환 횟수
☉ 외부 루프의 각 단계마다 (i+2)번의 이동 발생
☉ n(n-1)/2 + 2(n-1) = (n^2+3n-4)/2 = O(n^2)
☉ Worst T(n) = O(n^2)
🧪 정렬 알고리즘의 특징별 분류
◈ 정렬 수행시 데이터 저장 위치에 따른 분류
☉ 내부 정렬 (internal sort)
☉ 정렬 전 모든 데이터가 주기억장치에 올라와있음
☉ 따라서, 대용량 데이터에는 적용 어려움
☉ 例) 교환 정렬, 삽입 정렬, 선택 정렬 등
☉ 외부 정렬 (external sort)
☉ 정렬 전 모든 데이터가 외부기억장치에 있고,
☉ 필요시 일부분씩 만 주기억장치에 올려 정렬
☉ 속도가 느린 외부 보조기억장치를 사용하므로, 내부 정렬 보다 느림
☉ 例) 병합 정렬 등
◈ 정렬 수행시 저장공간 필요량에 따른 분류
☉ 제자리 정렬 (in-place sort : in-place 정렬)
☉ 입력 자료에 할당된 메모리 이외 일정 상수 만큼 작은 추가 메모리 만 필요
☉ 즉, 입력 크기가 커지더라도 추가 저장공간이 필요치 않음
☉ 例) 교환 정렬, 삽입 정렬, 선택 정렬, 힙 정렬 등
◈ 정렬의 안정함에 따른 분류
☉ 안정함 (stable sort : 안정 정렬)
☉ 입력 자료의 순서 그대로 정렬
☉ 입력 자료 키 값이 같을 경우에도, 입력되는 순서 그대로 유지됨
☉ 例) 버블 정렬, 병합 정렬 등
☉ 안정하지 못함 (nonstable sort)
☉ 입력 자료의 순서가 바뀔 수 있는 정렬
☉ 다중 키 정렬시, 먼저 정렬한 내용이 보존되지 않는 경우
☉ 例) 선택 정렬, 퀵 정렬 등
🧪 제자리 정렬
🔹 in-place 정렬은 추가적인 공간이 필요하지 않은 정렬이다. merge sort나 quick sort 처럼 요소를 분할하면서 추가적인 공간을 필요로 하지 않은 정렬이다. 현재 배열 안에서 정렬이 다 이뤄지는 것이다. 이러한 정렬에는 버블, 삽입, 선택, 힙 정렬 등이 있다.
이 중에서 퀵 정렬(Quick Sort)은 전통적으로 제자리 정렬 알고리즘은 아니다. 퀵 정렬은 일반적으로 추가적인 공간을 사용하여 정렬을 수행하며, 분할 정복(divide and conquer) 방식을 사용하여 배열을 정렬한다. 그러나 퀵 정렬을 제자리 정렬로 변형할 수 있는 방법이 있다. 이를 위해서 재귀적인 호출을 줄이거나, 추가적인 공간을 사용하지 않고도 배열 내에서 요소의 위치를 변경하는 방법을 사용해야 한다. 이런 변형들을 통해 제자리 퀵 정렬(In-place Quick Sort)을 만들 수 있다.
in-place 정렬의 경우, 연속된 메모리를 한 번 받아 더 이상 메모리를 할당 받는 일이 없다. 한 번에 연속된 메모리에서 데이터들이 저장되는 것이다. 반면 in-place 정렬이 아닌 퀵이나 합병 정렬의 경우, 새로운 메모리를 계속 할당 받는데, 이러한 메모리들은 연속적이지 않아 지역성이 좋지 못하다.
이러한 in-place 정렬의 공간 지역성 덕분에, Insertion 정렬의 경우 소수의 원소들을 정렬할 때 merge나 quick보다 더 좋은 성능을 보인다. 이러한 점을 활용하여 Tim sort가 탄생한 것이다. 기존의 merge sort가 원소가 1개가 될 때까지 쪼갰다. 하지만 Tim sort는 1개가 아니라 swift의 sort 기준으로 64개가 될 때까지 쪼갠다. 그리고 64개를 insertion sort로 정렬한다.
🧪 안정 정렬
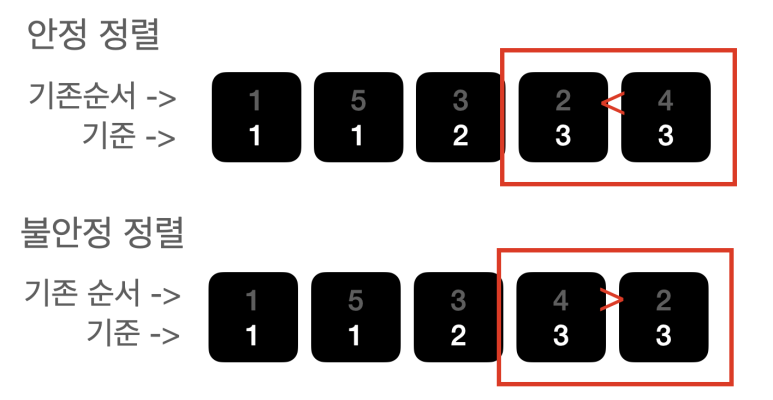
🔹 안정 정렬은 기준 값이 같을 때 기존의 순서대로 유지된 것을 확인할 수 있다. 반면, 불안정 정렬의 경우 기준 값이 같을 때 기존의 순서가 보장이 되지 않는다. 2는 기존에 4 앞에 있던 원소다. 그런데 정렬 후 4 뒤로 이동하였다. '보장하지 않는다'라고 하였으니 순서가 유지 되는 경우도 있다. 그래서 기준이 1일 때 처럼 순서가 보장된 경우도 있는 것이다.
다음 알고리즘들은 '안정 정렬'이다.
-> 버블 정렬, 삽입 정렬, 병합 정렬
다음 알고리즘들은 '불안정 정렬'이다.
-> 선택 정렬, 퀵 정렬, 힙 정렬
안정 정렬과 불안정 정렬을 구분해야하는 이유는?
예를 들어, 학년을 기준으로 정렬한다고 생각해보면 이때 학년이 같은 학생끼리는 어떻게 정렬이 되어야 할까. 만약 unstable하다면 학년을 기준으로 분류만 되고, 같은 학년 내에 있는 학생 정보는 뒤죽 박죽 섞여버릴 것이다. 기존에 이름을 기준으로 정렬이 되어 있었다고 할지라도 unstable한 정렬로 학년 정렬을 진행하면 이름 차순이 깨져버린다. 반면 stable한 정렬을 하게 되면, 같은 학년 내에서 이름차순이 유지되어 있을 것이다.
이런식으로 stable한 정렬과 unstable한 정렬은 큰 차이를 가지고 있다. 뭐가 더 좋다라는 기준이 있는 것은 아니지만 이왕이면 stable한 것이 더 나아 보인다. 기존의 순서를 보장해준다는 것은 분명한 이점이 있다. 정렬의 기준이 여러 개라면, 이 정렬을 그냥 이어서 해주면 된다. 앞에 순서가 보장이 되기 때문이다. 하지만 불안정하다면 여러 개의 기준으로 정렬하는 것이 힘들어진다. 그리고 unstable하다고 해서 성능이 더 나은 것도 아니다.
📸 참조
https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html
https://gyoogle.dev/blog/algorithm/Bubble%20Sort.html
https://blog.naver.com/wjdwoaud159/222365210954
http://www.ktword.co.kr/test/view/view.php?m_temp1=522
'Hub Development > Computer Science' 카테고리의 다른 글
| [CS] RDB와 NoSQL에서의 클러스터링/리플리케이션 방식 (CS 스터디 - DB 4주차) (0) | 2024.03.28 |
|---|---|
| [CS] Transaction Concurrency Control (CS 스터디 - DB 3주차) (2) | 2024.03.22 |
| [CS] Stack & Queue (CS 스터디 - 자료구조 1주차) (0) | 2024.03.07 |
| [CS] CPU 스케줄링 (2) | 2024.02.21 |
| [CS] 프로세스 메모리 구조 (2) | 2024.01.29 |



